Research
Path probabilities for diffusive stochastic dynamics
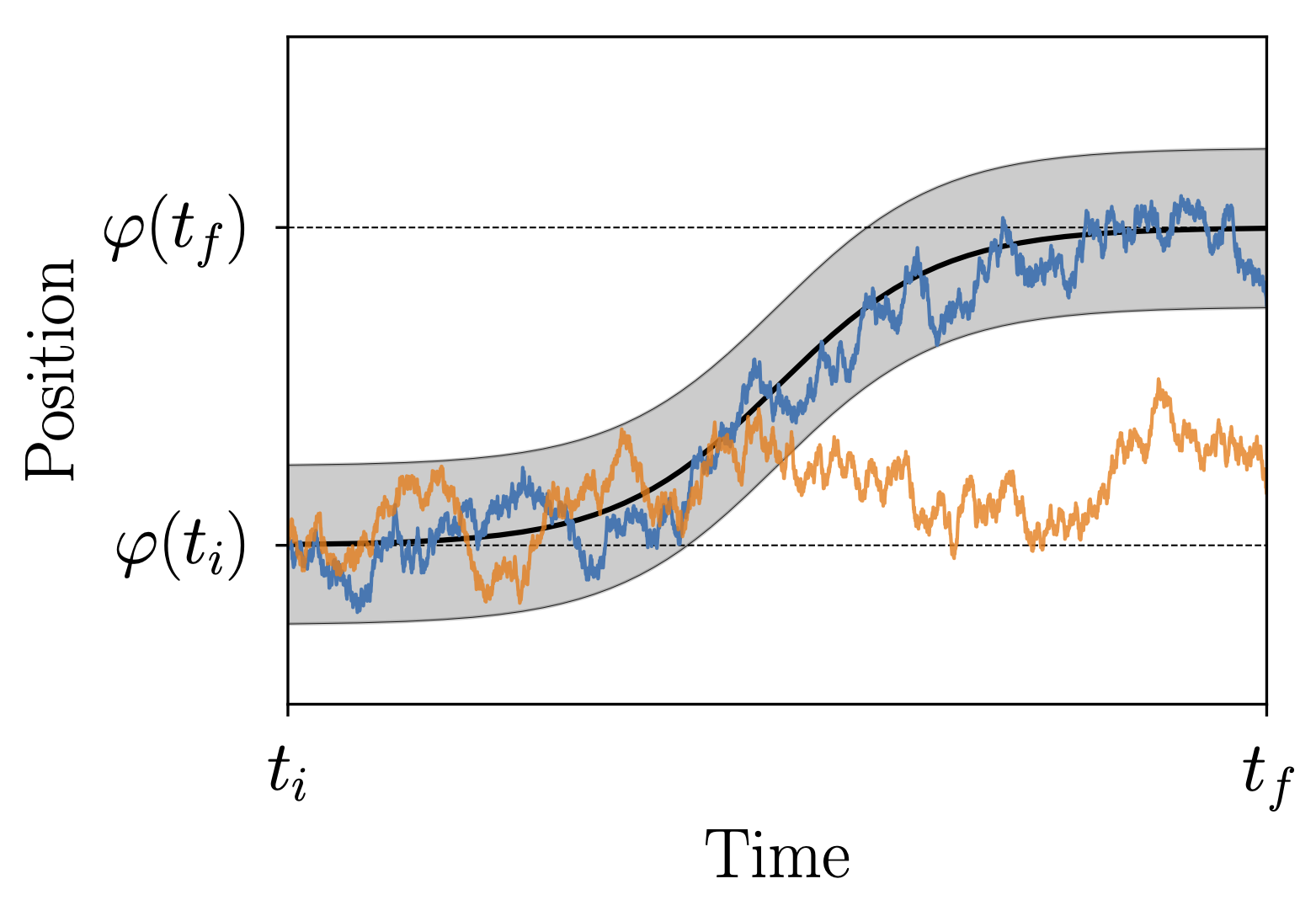
Technically speaking, the probability to observe a given individual stochastic trajectory vanishes, much like the probability of a given number is zero for many continuous probability distributions such as e.g. the Gaussian distribution. This makes it unclear how to measure path probabilities, because only events that occur with positive probability are accessible experimentally. To connect the discussion of path probabilities to measurement, we consider the tubular ensemble, comprised of all stochastic trajectories that remain within a tubular neighborhood of a given reference path. While in the limit of vanishing tube radius only the reference path remains in the tubular ensemble, for finite tube radius the probability to observe any of the trajectories of the tubular ensemble is positive. The tubular ensemble for small-but-finite radius is hence an experimentally accessible surrogate for probing any question that can be asked about paths for diffusive stochastic dynamics.
Related key publications:
- “Stochastic action for tubes: Connecting path probabilities to measurement”, J. Kappler, R. Adhikari, Physical Review Research, vol. 2, p. 023407, 2020. DOI: 10.1103/PhysRevResearch.2.023407
- “Experimental Measurement of Relative Path Probabilities and Stochastic Actions”, J. Gladrow, U. F. Keyser, R. Adhikari, J. Kappler, Physical Review X, vol. 11, p. 031022, 2021. DOI: 10.1103/PhysRevX.11.031022
- “Experimental Measurement of Relative Path Probabilities and Stochastic Actions”, J. Gladrow, U. F. Keyser, R. Adhikari, J. Kappler, Physical Review X, vol. 11, p. 031022, 2021. DOI: 10.1103/PhysRevX.11.031022
- “Sojourn probabilities in tubes and pathwise irreversibility for Itô processes”, J. Kappler, M. E. Cates, R. Adhikari. arXiv: 2009.04250
- “Resolution dependence of most probable pathways with state-dependent diffusivity”, A. L. Thorneywork, J. Gladrow, U. F. Keyser, M. E. Cates, R. Adhikari, J. Kappler. arXiv: 2402.01559
Related Python modules:
- PyTubular: Python module for the evaluation of probability densities and exit rates in the tubular ensemble
- Cloning algorithm for measuring rare events from stochastic time series
- Fokker-Planck: Python module for numerical solution, calculation of spectra, and parameter inference for the 1D Fokker-Planck equation
Waves at interfaces
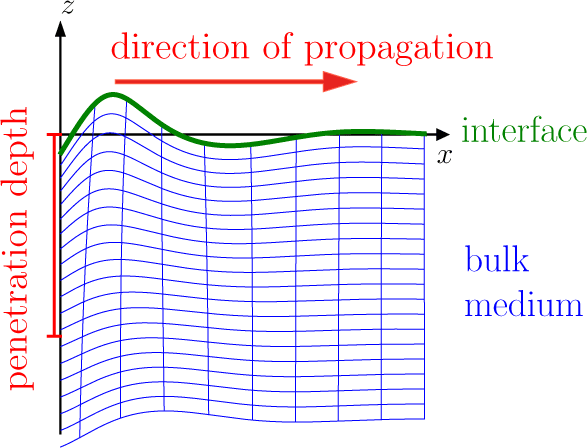
Everybody is familiar with capillary-gravity surface waves, which can for example be excited by throwing a stone in water. A second kind of surface wave can exist if the surface has an elastic response, which is for example the case if a fluid is covered by a biomembrane. This wave is basically a 2D sound wave which propagates along the elastic interface, but because of the coupling to the underlying fluid its properties are very different from the usual sound waves in 3D. We showed that this 2D sound wave obeys a fractional wave equation, and found an intuitive explanation for the appearance of the fractional derivative in this context.
Related Publications:
- “Multiple surface wave solutions on linear viscoelastic media”, J. Kappler and R. R. Netz, Europhysics Letters, vol. 112, p. 19002, 2015. DOI: 10.1209/0295-5075/112/19002
- “Nonlinear fractional waves at elastic interfaces”, J. Kappler, S. Shrivastava, M. F. Schneider, and R. R. Netz, Physical Review Fluids, vol. 2, p. 114804, 2017. DOI: 10.1103/PhysRevFluids.2.114804
- “Linear waves at viscoelastic interfaces between viscoelastic media”, S. Zendehroud, R. R. Netz, and J. Kappler, Physical Review Fluids, vol. 7 (11), p. 114801, 2022. DOI: 10.1103/PhysRevFluids.7.114801